Can Light (Or Photons) Form Orbits Around A Black Hole?

Black holes generate one of the strongest gravitational forces in the universe. It is so powerful that it can make light orbit around it.

A black hole has extreme gravitational attraction due to its incredibly high density. With its event horizon being the point of no return and trapping even light, it draws in a lot of extreme and high-energy physics around it.

Now, you probably already know that light can’t escape the clutches of a black hole once it enters the event horizon. Therefore, it seems possible that light might also fall into orbit around a black hole. Physicists have even termed certain spherical regions around black holes “photon spheres”.

This is probably one of the weirdest regions in the universe, with physicists speculating that once you are inside the photon orbit, you might be able to see the back of your head!

In this article, we will try to understand how these orbits would look and how the nature of a black hole would affect the path of these photons around a black hole. For that, we need to look at the properties of the black holes.

Recommended Video for you:

No-hair Theorem And Black hole types

From a theoretical perspective, we can depict black holes using three quantities: mass, spin and charge. This property of a black hole, where we characterize it using just three numbers, is commonly known as the no-hair theorem.

Physicists developed mathematical models that would help explain the gravitational properties of black holes with these features. For example, the German physicist, Karl Schwarzschild, developed equations describing the regions around a stationary, non-rotating black hole with zero charges. Schwarzschild achieved this by solving the famous Einstein field equations in general relativity. Such black holes (non-rotating and charge-free) are now called Schwarzschild black holes.

Similarly, New Zealander mathematician, Roy Kerr, was the first to describe the region of space (and time) around and the gravitational effect of a rotating black hole without any charge. Such types of black holes are correspondingly called Kerr black holes.

Finally, black holes containing charges but no spin are referred to as Reissner-Nordstrom black holes, while black holes with both electric charge and spin are called Kerr-Newman black holes. We have named them after those physicists who solved the Einstein field equations for such black holes. The solutions they obtained can describe the gravitational effect of the black holes on objects around them.

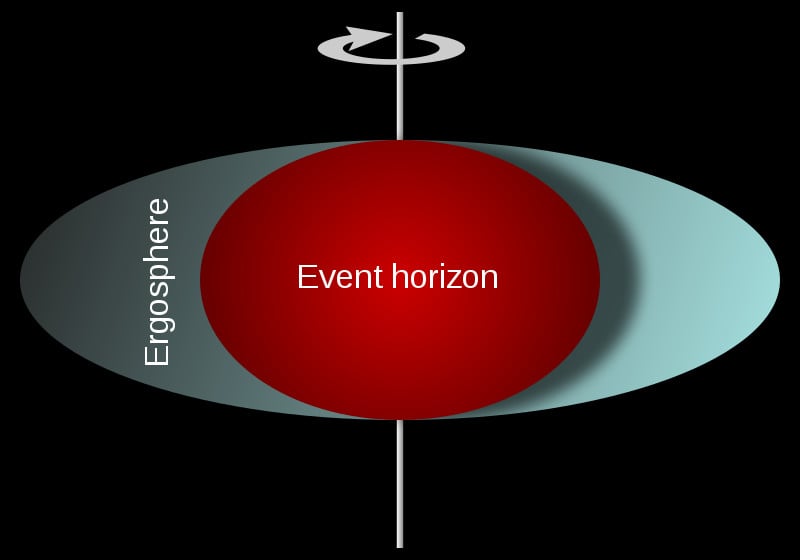
It is worth mentioning that the formulation of the no-hair theorem happened after the discovery and publication of the above-mentioned black holes. Here, we will discuss photon orbits in the case of Schwarzschild, Kerr and Kerr-Newman black holes.

Photon Orbits For Schwarzschild Black Holes

Now, onto photon spheres. This is a spherical region having a radius of about 3GM/c² meters away from the center of the black hole, where G is the universal gravitational constant, M is the black hole’s mass, and c is the speed of light. It is important to note that this applies only to Schwarzschild black holes and not to the other types. A photon can be in any one of the circular orbits present on the photon sphere, which could have various inclinations.

In a Schwarzschild black hole, the circular light orbits formed in the photon sphere are relatively unstable. This means that if we disturb a photon in orbit around a Schwarzschild black hole, then it will no longer orbit it. Photons that go even slightly below this orbit will fall into the black hole, whereas if it goes just a little above, it will get launched away into outer space.

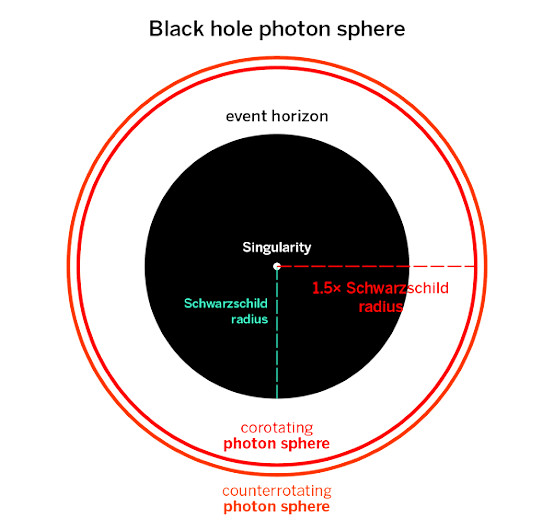
So, what about the other kinds of black holes? Well, the math starts getting complicated from this point onwards. As we start accounting for each property (first spin, and then both spin and charge, etc.), it gets increasingly difficult to obtain the radii of the photon orbits, their stability, and their energies.

Photon Orbits For Kerr And Kerr-Newman Black Holes

In the case of Kerr black holes, several spherical orbits are possible. From these orbits, two are just the usual circular orbits lying along the rotating black hole’s equator, one of which will be along the same direction in which the black hole spins, while the other will be in the opposite direction.

However, the other types of orbits are not exactly circular. While their paths are at a fixed distance from the black hole, the orbit exists on a spherical surface, often with a helix-like appearance. When viewed from the side of the black hole, some of these orbits oscillate between two fixed latitudes centered about the equator. Other orbits appear along the longitudes, passing nearly close to the poles of the black hole.

Since such orbits are along the surface of a sphere surrounding the black hole, they are referred to as spherical orbits. While the orbit itself is at a fixed distance from the black hole, the different orbits will be at different radial distances from the black hole, depending on the black hole’s properties, like its mass and rotational speed.

When it comes to Kerr-Newman black holes, the orbits will also have to account for both the charge and spin of the black hole. Theoretically, physicists have found that one possible spherical orbit could pass through the poles of the black hole. There are also two or three circular orbits along its equator, which depend on the charge and rotation rates of the black hole.

In other cases, where the orbits are neither along the equator nor across the poles, there are usually one or two such spherical orbits. The number depends on how inclined it is with respect to the equator. If its inclination is above a certain value (called the critical inclination angle), then there can be two possible spherical orbits. If it is less than that value, then there is only one such spherical orbit. The value of the critical inclination angle is strongly dependent on the rotation rate of the black hole.

Some Caveats

In the above cases, we considered the black holes as standalone entities. In reality, these photon orbits might also depend on other external factors. One such situation is that supermassive black holes usually have disks of matter and radiation surrounding them. Some of this would move past the event horizon and increase the mass of the black hole. It would, in turn, affect photon orbits.

We have also not accounted for quantum effects at the boundary of the event horizon, including things like Hawking radiation. Whatever this article has presented above is strictly from a general relativity point of view.

However, in most cases, physicists think (or at least assume) that a Kerr black hole would easily describe a real black hole. There is research that attempts to determine the exact shapes of these orbits to verify with possible observations of photon orbits we might obtain in the future. Some predictions account for deviations occurring from other effects in the black hole environment. While detecting them may be difficult, as a photon in orbit around the black hole would probably never reach us, it does pose a valuable way to test our theories on black holes and even help uncover new realms of physics!