What Are Cooper Pairs & How Are They Responsible For Superconductivity?

Cooper pairs are a pair of electrons with opposite spins that are loosely bound at absolute temperatures due to electron-lattice interactions. Their condensation to bosonic states at low temperatures is believed to be the reason behind superconductivity.

From two oppositely-minded humans falling in love to subatomic particles with the same net charge repelling each other, the belief that ‘opposites attract and likes repel’ is known to have universal implications. However, when this so-called law decides to make an exception, something ‘super’ ensues.

Superconductivity—a state wherein a conductor conducts electricity with zero resistance—is believed to be a result of two electrons (negatively charged subatomic particles) bonding instead of repelling each other. This bond materializes at extremely low absolute temperatures and the bound electrons are jointly known as a Cooper pair.

Recommended Video for you:

Superconductivity

As mentioned earlier, superconductivity is a physical state in which a conductor loses all electrical resistance. The phenomenon was discovered by physicist Heike Onnes in 1911 while studying the temperature dependence of resistance in mercury. While cooling mercury at 4.2 K (-268.95°C), he noticed that all electrical resistance suddenly vanished. Following Onnes’ discovery of superconductivity, in subsequent years, researchers found other elements and alloys that reflected this same behavior at extreme absolute temperatures.

Electrical resistance, as you may know, is an obstruction to the flow of electrons (current) caused by the vibrational motion of crystal lattice. The amount of resistance depends on a variety of factors, including geometry, composition and temperature. Of the three, an increase or decrease in temperature is mirrored by the resistance of the conductor, whereas semi-conductors have a negative temperature coefficient and do not follow this trend.

As the temperature of the conducting material is raised, the lattice atoms start vibrating more rigorously, further obstructing the flow of electrons. On the flip side, when a conductor is cooled, atoms vibrate with less intensity and therefore have lower resistance to current.

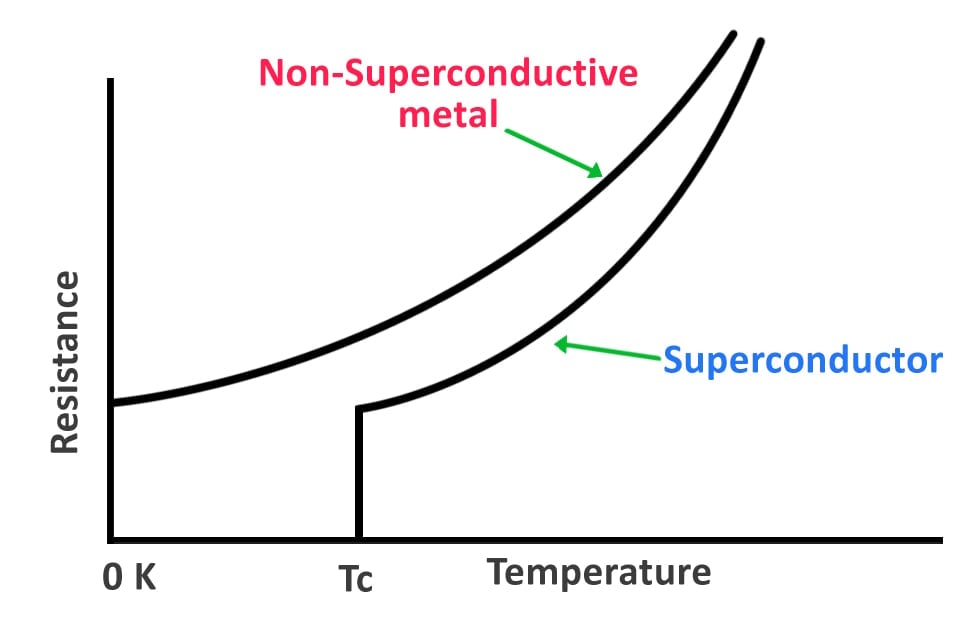
However, the linear relationship between resistance and temperature is only maintained up to a specific value, after which all resistance suddenly disappears and the transition to the superconducting state occurs. The temperature at which this transition from a regular conductor to a superconductor happens is known as the critical temperature (T_c). Critical temperatures for most elements lie between 0K and 30K (-273.15°C to -243.15°C), but some materials with critical temperatures over 35K (-238.15°C) have also been identified.

Meissner Effect

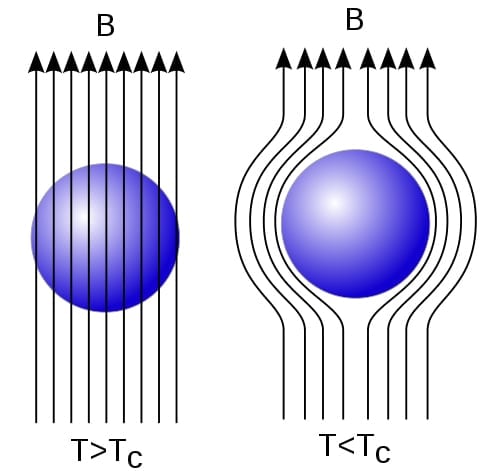
Another strange phenomenon exhibited by a superconductor is the expulsion of an external magnetic field from its inner parts, which is commonly known as the Meissner Effect. This expulsion occurs due to the development of an equal and opposite magnetic field by the surface currents inside the superconductor. This field cancels the applied magnetic field, making the superconductor exhibit perfect diamagnetism. This is best demonstrated by placing a magnet on a superconductor; the two magnetic fields oppose each other, causing the magnet to levitate above the superconductor.

Also, a sudden spike in the heat capacity of the superconducting material vanadium has been observed when approaching the critical temperature.

The sudden disappearance of resistance opposed to a linear progression, the expulsion of an external magnetic field and the increase in heat capacity suggests that there are more forces at work—perhaps even a phase change of matter.

Cooper Pair & BCS Theory

The world had to wait quite some time for scientists to unravel the mysteries of superconductors. In 1957, physicists John Bardeen, Leon Cooper, and John Robert Schrieffer came up with the first microscopic theory to explain the genesis of superconductors. The theory states that superconductivity results from the formation and condensation of multiple electron pairs, known as Cooper pairs.

Electrons may repel fellow electrons, but they are also believed to exert an attractive force on the positive ions that make up the crystal lattice (arrangement of atoms, ions or molecules). According to the BCS theory, this attraction draws the positive ions closer to the passing electron, resulting in a region of higher positive charge density. As the electron moves, so does this region of higher positive charge density. The region, in turn, attracts another electron with an opposite spin than the first. The two electrons thus become indirectly linked and form a Cooper pair thanks to their “atomic Cupid”, the crystal lattice.

The possibility of electron-lattice interaction is also supported by the isotope effect, which was witnessed in superconductors a few years earlier. Affirmed by the results produced by two separate groups, using a different isotope of the same superconducting element was seen to shift the critical temperature. Heavier ions are considered harder for electrons to attract/pull, so the critical temperature was found to be inversely proportional to the mass of the isotope.

The paired electrons are not actually in close proximity to each other, but are instead paired over several hundred nanometers. This allows multiple Cooper pairs to occupy the same space, overlap, and form a collective condensate. Also, the binding energy is quite low, of a magnitude 10⁻³ eV.

Condensation Of Cooper Pairs

In reality, the formation of Cooper pairs and their influence on superconductivity is a complex quantum phenomenon requiring knowledge of quantum mechanics to fully comprehend. Nevertheless, here we go.

The existence of critical temperature, critical magnetic field (a superconductor stops exuding a magnetic field beyond the critical magnetic field), and an increase in heat capacity when approaching the critical temperature suggests the presence of an energy gap between the conducting and superconducting state. In semiconductors, a similar energy gap (known as a bandgap) exists between the valence band and the conduction band, but in superconductors, the energy gap represents the amount of energy required to break Cooper pairs and form normal electrons. The energy gap also hints at a change of phase, suggesting that all electrons must be occupying the same energy level.

Electrons are fermions, i.e, particles with half-integer spins, and cannot condense into the same energy level. However, when two electrons link up to form a Cooper pair, their opposite spin values are thought to balance/cancel each other out, resulting in a net integer spin for the pair. The existence of a similar energy gap had been previously seen in superfluid helium, although it is composed of bosons (particles with integer spin values). Therefore, Cooper pairs are believed to act like composite bosons and can therefore condense to the same quantum state.

At low absolute temperatures, the thermal energy available is not sufficient to break Cooper pairs and thus prevents the kind of electron-lattice interaction that leads to resistivity. Also, since Cooper pairs overlap, they become entangled and act as one big group of current-carrying particles.

The formation of Cooper pairs due to the interaction of electrons with the crystal lattice, along with their condensation to act as composite bosons, is thus believed to be the reason for superconductivity.

Final Words

The trio of John Bardeen, Leon Cooper, and John Robert Schrieffer were awarded the Nobel Prize in physics for putting forth the BCS theory and thus helping to explain the behavior of superconductors. However, a few decades after the BCS theory was proposed, certain materials were discovered to exhibit superconductivity at temperatures above 30K (Type 2 superconductors, also known as high-temperature superconductors). This behavior can’t be completely explained using the BCS theory and remains a mystery.

Currently, the applications of superconductivity are limited due to the extreme critical temperatures that must be attained for Type 1 superconductors and the limited knowledge of how Type 2 superconductors work. Having said that, superconductivity finds employment in MRI & NMR machines, particle accelerators, SQUIDS and maglev trains, among other exciting modern applications!