What Is The Infinite Hotel Paradox?

Mathematicians and scientists have always been intrigued by the mysteries behind ‘infinity’. The Hilbert’s paradox of an infinite hotel is one such thought experiment that arouses curiosity and intrigues people to this day.

Imagine that your boss asked you to go on an urgent business trip to one of the busiest places in the country. The first thing you would do is book your tickets and look up a hotel with available rooms. Alas! After two hours of searching, you find that all the hotels are full.

Suddenly, an ‘Infinite Hotel’ advertisement comes up, so you visit the website and manage to find a room for yourself, even if the hotel is full.

Now, you might begin to wonder… what is this infinite hotel exactly? How is it possible that, despite having no vacancy, vacant rooms can still be arranged for guests? It’s contradictory to logic!

Recommended Video for you:

Infinity Is Vague

The concept of infinity is interesting and requires you to have an open mind while exploring various aspects of it. Mathematics is such that it needs you to give up your pre-assumed notions and dive into the unknown.

Infinity is a vague concept that implies endless possibilities, giving rise to a huge number of paradoxes. It could be appropriate to say that mathematicians have made this concept even more complex by introducing terms like ‘countably infinite’ and ‘uncountably infinite’.

On the one hand, we say that infinite things are unbounded and unfathomable, implying ‘uncountable infinite things’, and on the other hand, we consider a very large collection of things as ‘countably infinite’, which can be counted one at a time, even though it’s counting won’t come to an end. Isn’t that strange?

The ‘Infinite Hotel Paradox’

The ‘Infinite Hotel Paradox’ is one such thought experiment proposed by David Hilbert in 1924 that explores the infinite nature of numbers and the properties of an infinite set.

Let’s assume that there is a grand hotel called the ‘Infinite Hotel,’ which has a countably infinite number of occupied rooms. The rooms correspond to the natural numbers in the number series. Using common sense, one would conclude that since the hotel is completely occupied, no more guests can be accommodated, but here comes the twist with “infinity”.

Infinity is unbounded, so no matter how big the number is, there is always a bigger number. Thus, if you want a room there, the hotel manager can easily arrange it for you.

But how does the manager do it? If you think about it, you might come up with one answer to this paradox. You can say that since there is an infinite number of rooms, the guest can simply be put in the last room…

… but wait, the mystery is not that easy to crack, since infinity is involved here. There is no last room in the infinite hotel!

The Tricky Solution

There is no last room, but there always exists the next room in this Infinite Hotel. And therein lies the solution to accommodating extra guests into new rooms.

The clever manager can shift each guest to the immediate next room, simultaneously. For example, move the guest from room #1 to room #2, room #2 to room #3, room #3 to room #4, and so on. In this way, the guest in room #n is shifted to room #n+1.

In this way, after shifting every guest, room #1 is empty, where one more guest can be accommodated.

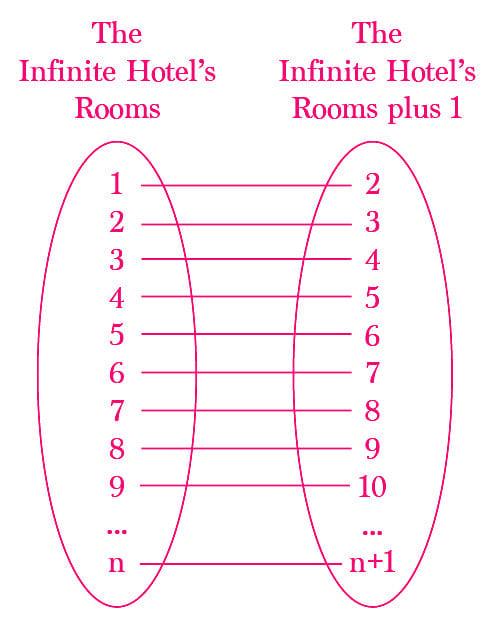
This method can be employed to free up any finite number of rooms to accommodate any finite number of guests in the hotel.

Will The ‘Infinite Hotel’ Ever Run Out Of Rooms?

The above was the thought experiment case for a finite number of guests.

What will the scenario be if an infinite number of guests want to check in? Will the infinite hotel run out of rooms? Mathematically speaking, no!

Let’s Consider Two Cases:

1) A Bus Arrives With An Infinite Number Of Passengers Seeking Rooms

The popularity of this hotel is on the rise, and one day a bus arrives with an infinite number of passengers who are in search of rooms in this hotel. The task falls on the shoulders of the manager to arrange rooms for them.

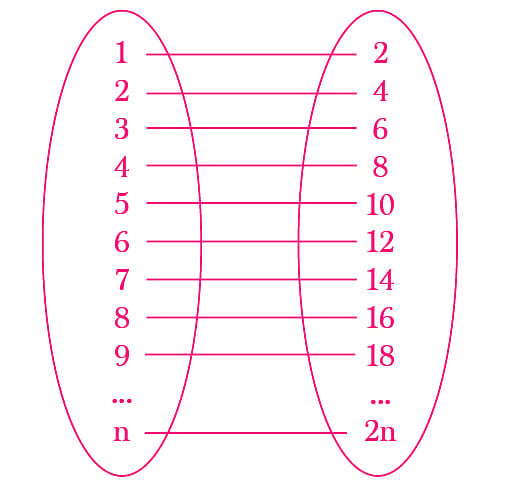
The clever manager is very good with mathematics and he finds the solution instantly. He shifts the guest in room #1 to room #2, in room #2 to room #4, in room #3 to room #6, and so on. In this way, the guest in room #n is shifted to room #2n.

This leaves the manager with an infinite odd number of empty rooms where the infinite number of passengers can be accommodated.

2) An Infinite Number Of Buses Arrive With An Infinite Number Of Passengers Seeking Rooms

On yet another evening, the manager is bewildered to see an infinite number of buses arriving with an infinite number of passengers seeking rooms. Now, this is the trickiest of all the cases to crack, but the manager is also clever enough to handle the challenge. He quickly remembers his mathematics lessons at school and realizes that the set of all prime numbers (2, 3, 5, 7, 11,…..) is countably infinite.

Thus, he begins shifting the infinite set of the current guests of the hotel from their current room numbers to room numbers that are equal to the power of the current room number raised to the base 2. So the person in room #1 is shifted to room #2^1= 2, the person in room #2 is shifted to room #2^2 = 4, and so on. In this way, the guest in room #n is shifted to room #2^n.

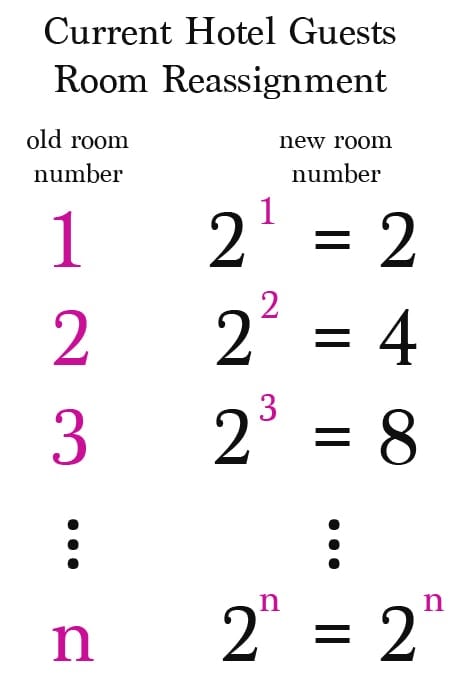
After this, the passengers of the first bus are assigned rooms by using the next prime number 3. The passenger in seat #1 is moved to room #3^1, the passenger in seat #2 is moved to room #3^2, and so on. In this way, the passenger in seat #n is moved to room #3^n.

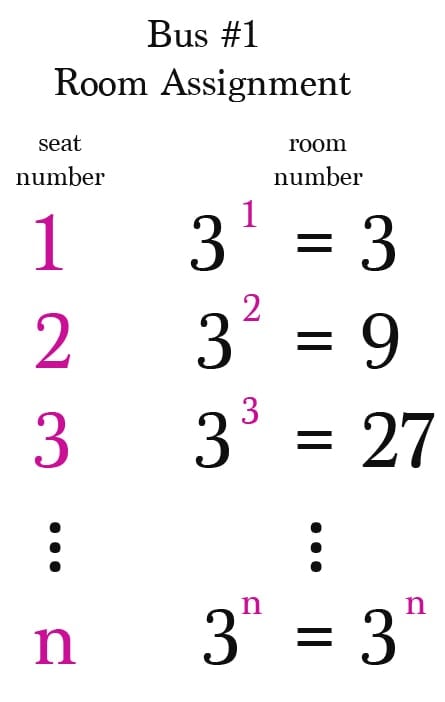
Similarly, the passengers of the second bus are assigned rooms by using the next prime number 5. The passenger in seat #1 is moved to room #5^1, the passenger in seat #2 is moved to room #5^2, and so on. In this way, the passenger in seat #n is moved to room #5^n.

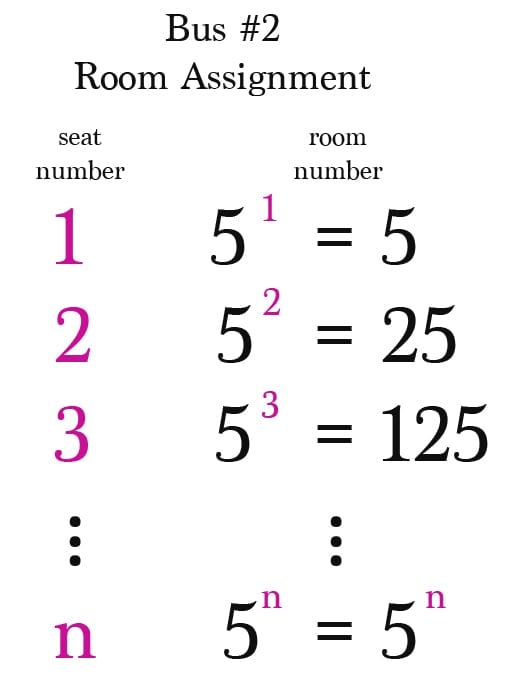
Employing this method, the manager effortlessly accommodates all the infinite number of passengers from the infinite number of buses. He should also get a salary raise for using such witty methods, don’t you think?

A Final Word

Believe it or not, even after accommodating an infinite number of guests, there will still be many rooms unoccupied in the ‘Infinite Hotel,’ which is pretty mind-blowing! To put it simply, the paradox lies in the contradiction of the statements that ‘the hotel is fully occupied’ and ‘there is still room for every new guest’, as both are true!

It certainly would be a blessing to find this ‘Infinite Hotel’ when you really need to find a room for an urgent and last-minute business meeting, right?